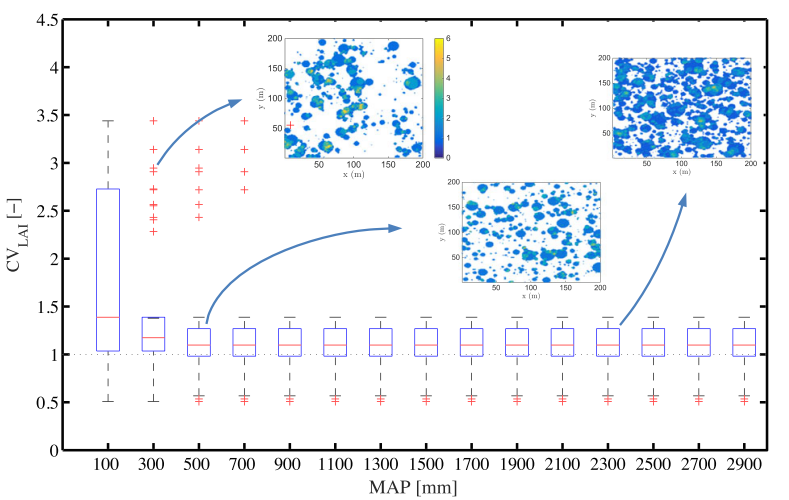
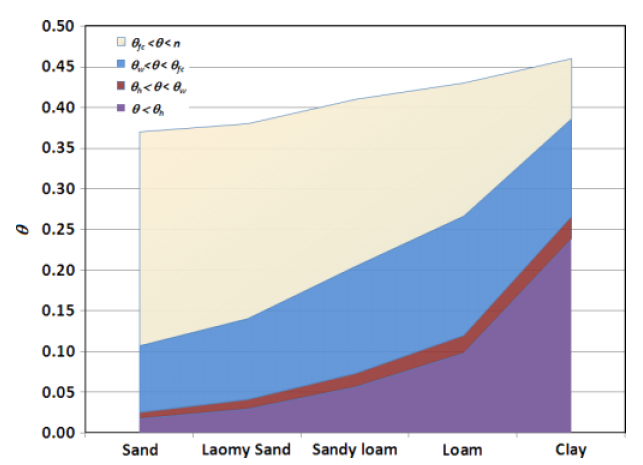
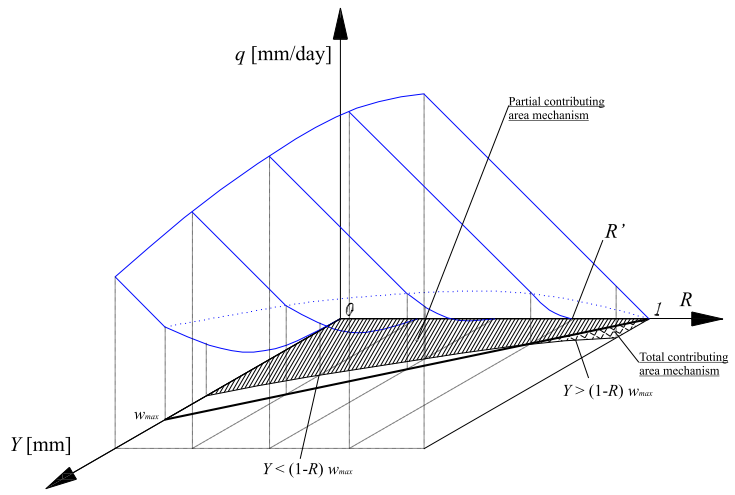
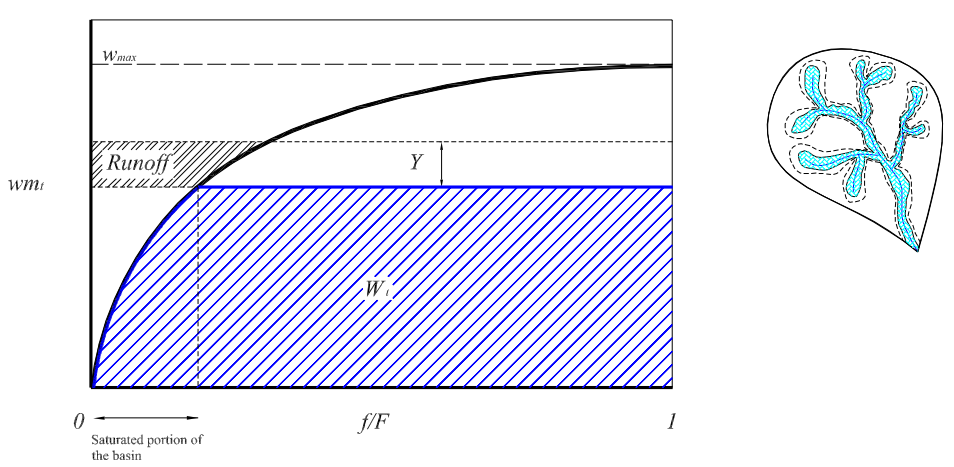
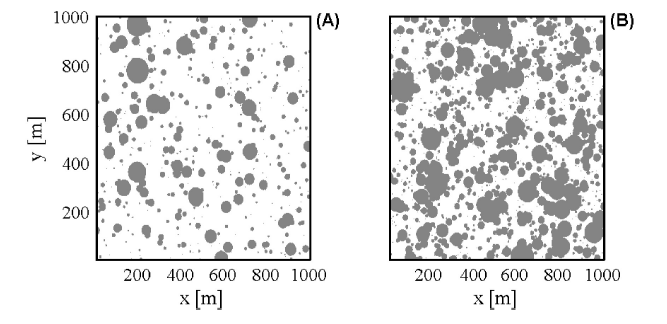
Spatial distribution of tracers for optical sensing of stream surface flow
River monitoring is of particular interest for our society that is facing increasing complexity in water management. Emerging technologies have contributed to opening new avenues for improving our monitoring capabilities,…