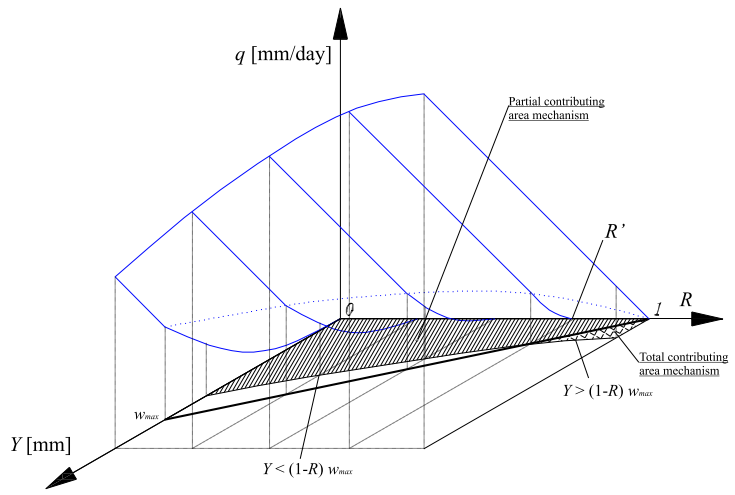
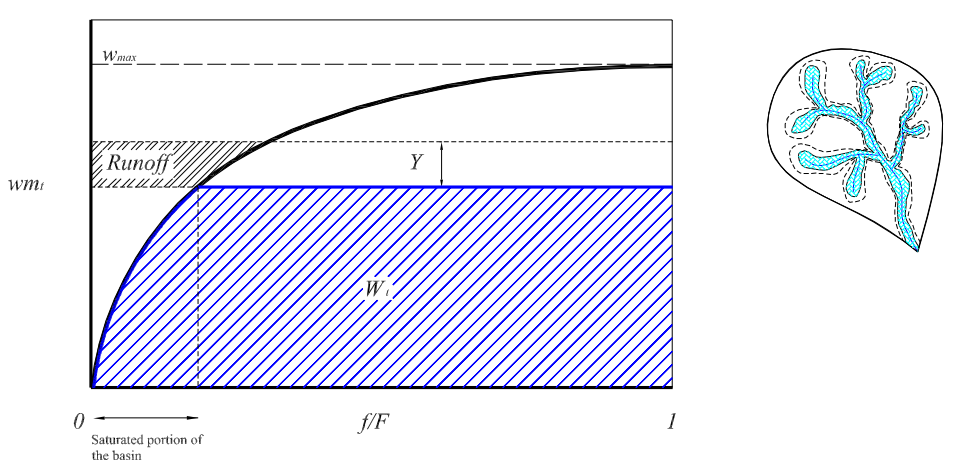
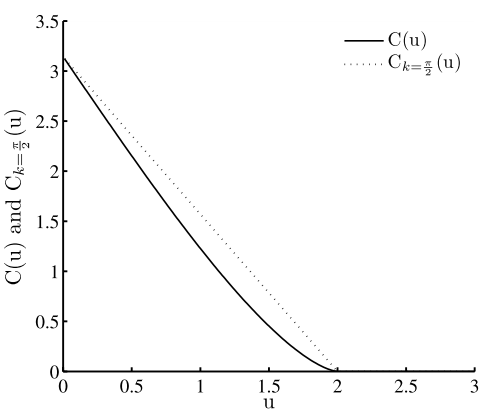
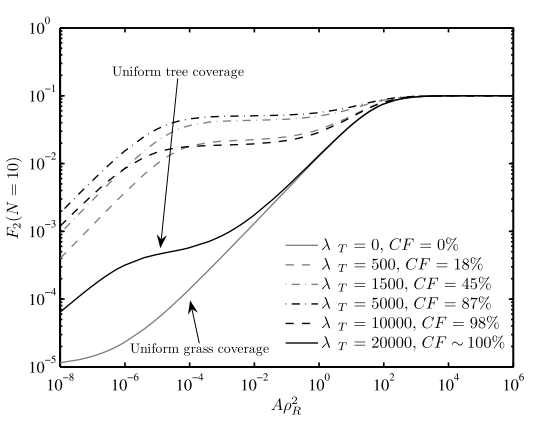
Stochastic Analysis of the Marginal and Dependence Structure of Streamflows: From Fine-Scale Records to Multi-Centennial Paleoclimatic Reconstructions
The identification of the second-order dependence structure of streamflow has been one of the oldest challenges in hydrological sciences, dating back to the pioneering work of H.E Hurst on the…